题目大意:n对字符串(a,b)和m个询问,每次询问是否可以将字符串s通过n个字符串替换成t,替换的前提是将s中a的部分替换成b得到t,问有多少种替换方案。
题目描述
对于字符串 $s$,定义 $s$ 的**替换**如下:
– 对于 $s$ 的某个子串 $y$,若存在 $1 \leq i \leq n$ 满足 $y = s_{i,1}$,则将 $y$ 替换为 $y’ = s_{i,2}$。具体地,设 $s = x + y + z$,其中 $x$ 和 $z$ 可以为空,“+” 表示字符串拼接,则 $s$ 的替换将得到字符串 $s’ = x + y’ + z$。
小 W 提出了 $q$ 个问题,第 $j$ ($1 \leq j \leq q$) 个问题会给定两个**不同**的字符串 $t_{j,1}, t_{j,2}$,她想知道有多少种字符串 $t_{j,1}$ 的替换能够得到字符串 $t_{j,2}$。两种 $s$ 的替换不同当且仅当**子串 $y$ 的位置不同或用于替换的二元组 $(s_{i,1}, s_{i,2})$ 不同**,即 $x, z$ 不同或 $i$ 不同。你需要回答小 W 提出的所有问题。
输入格式
输入的第 $j+n+1$ ($1 \leq j \leq q$) 行包含两个字符串 $t_{j,1}, t_{j,2}$,表示小 W 提出的第 $j$ 个问题。
输出格式
说明/提示
1. 令 $x, z$ 均为空串,$y = \text{xabcx}$, $i = 1$,则 $y’ = \texttt{xadex}$,替换后得到 $\text{xadex}$;
2. 令 $x = \texttt{xa}$, $y = \texttt{bc}$, $z = \texttt{x}$, $i = 3$,则 $y’ = \texttt{de}$,替换后得到 $\texttt{xadex}$。
### 【样例 3】
见选手目录下的 $replace/replace3.in$ 与 $replace/replace3.ans$。
该样例满足测试点 11, 12 的约束条件。
### 【样例 4】
见选手目录下的 $replace/replace4.in$ 与 $replace/replace4.ans$。
该样例满足测试点 15, 16 的约束条件。
### 【数据范围】
设 $L_1 = \sum_{i=1}^{n} |s_{i,1}| + |s_{i,2}|$, $L_2 = \sum_{j=1}^{q} |t_{j,1}| + |t_{j,2}|$。对于所有测试数据,保证:
– $1 \leq n, q \leq 2 \times 10^5$;
– $2 \leq L_1, L_2 \leq 5 \times 10^6$;
– 对于所有 $1 \leq i \leq n$, $s_{i,1}, s_{i,2}$ 均仅包含小写英文字母,且 $|s_{i,1}| = |s_{i,2}|$;
– 对于所有 $1 \leq j \leq q$, $t_{j,1}, t_{j,2}$ 均仅包含小写英文字母,且 $t_{j,1} \neq t_{j,2}$。
::cute-table{tuack}
| 测试点编号 | $n, q \leq$ | $L_1, L_2 \leq$ | 特殊性质 |
| :–: | :–: | :–: | :–: |
| $1, 2$ | $10^2$ | $200$ | 无 |
| $3 \sim 5$ | $10^3$ | $2\,000$ | ^ |
| $6$ | ^ | $10^6$ | AB |
| $7, 8$ | $10^4$ | ^ | A |
| $9, 10$ | $2 \times 10^5$ | ^ | B |
| $11, 12$ | ^ | $2 \times 10^6$ | 无 |
| $13, 14$ | ^ | $5 \times 10^6$ | A |
| $15, 16$ | ^ | ^ | B |
| $17 \sim 20$ |^ | ^ | 无 |
特殊性质 A:$q = 1$。
特殊性质 B:定义字符串 $s$ 为**特别的**,当且仅当字符串 $s$ 仅包含字符 $a$ 和 $b$,且字符 $b$ 在 $s$ 中出现**恰好**一次。对于所有 $1 \leq i \leq n$, $s_{i,1}, s_{i,2}$ 均为特别的,且对于所有 $1 \leq j \leq q$, $t_{j,1}, t_{j,2}$ 均为特别的。
解题思路
问题的本质是字符串a和字符b分别包含字符串s和t中不同的部分,即遇到不同部分时,a跟s匹配,b跟t匹配。
不妨设a串为AXB,b串为AYB,s串为SXT,b串为SYT,替换成功的前提是A是S的后缀,B是T的前缀。
我们可以将a和b转换成A#X#Y#B,s和t串转换为S#X#Y#T,这样只需要A#X#Y#B是S#X#Y#T的子串就行,直接跑AC自动机模板即可,内存限制2G不怕爆空间。
程序实现
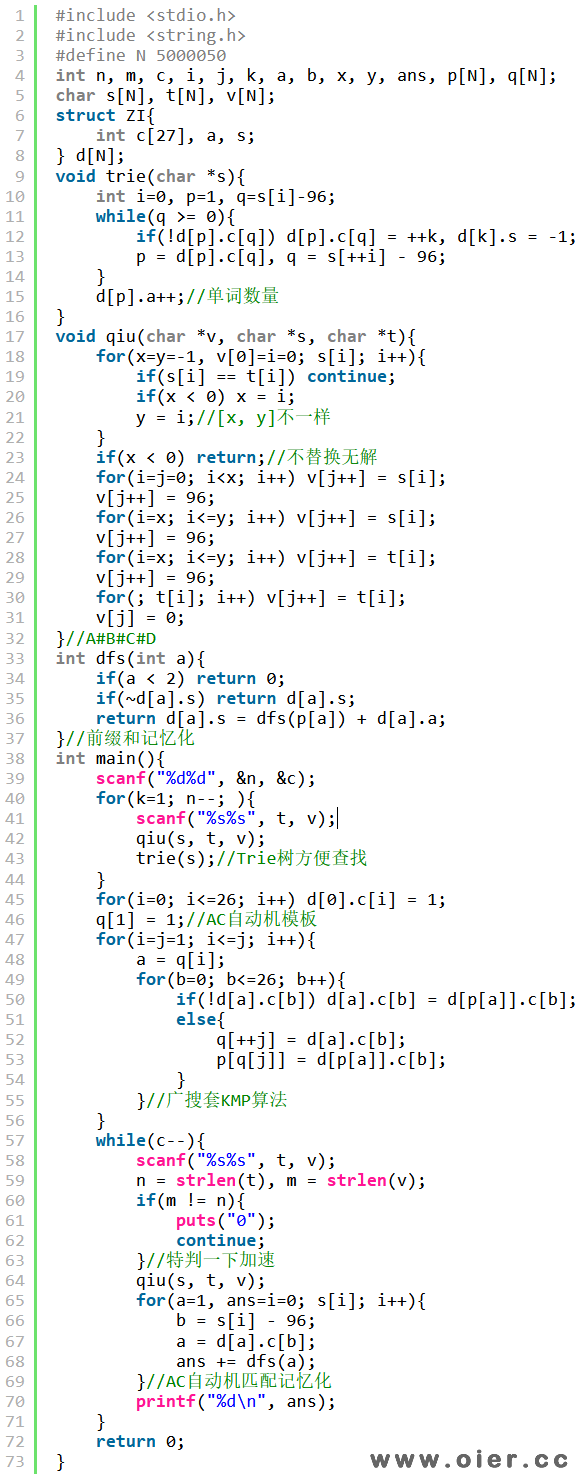
原来是这样用的 😉