题目大意:n跟小木棍,长度为$a_i$,能拼出多少种不同的多边形?(只要有一根木棍编号不同就是不同)
题目描述
小 R 喜欢玩小木棍。小 R 有 $n$ 根小木棍,第 $i$ ($1 \leq i \leq n$) 根小木棍的长度为 $a_i$。小 X 希望小 R 从这 $n$ 根小木棍中选出若干根小木棍,将它们按任意顺序首尾相连拼成一个多边形。小 R 并不知道小木棍能拼成多边形的条件,于是小 X 直接将条件告诉了他:对于长度分别为 $l_1, l_2, \dots, l_m$ 的 $m$ 根小木棍,这 $m$ 根小木棍能拼成一个多边形当且仅当 $m \geq 3$ 且所有小木棍的长度之和**大于**所有小木棍的长度最大值的两倍,即 $\sum_{i=1}^{m} l_i > 2 \times \max_{i=1}^{m} l_i$。
由于小 R 知道了小木棍能拼成多边形的条件,小 X 提出了一个更难的问题:有多少种选择小木棍的方案,使得选出的小木棍能够拼成一个多边形?你需要帮助小 R 求出选出的小木棍能够拼成一个多边形的方案数。两种方案不同当且仅当选择的小木棍的**下标集合不同**,即存在 $1 \leq i \leq n$,使得其中一种方案选择了第 $i$ 根小木棍,但另一种方案未选择。由于答案可能较大,你只需要求出答案对 $998,244,353$ 取模后的结果。
输入格式
输入的第一行包含一个正整数 $n$,表示小 R 的小木棍的数量。输入的第二行包含 $n$ 个正整数 $a_1, a_2, \dots, a_n$,表示小 R 的小木棍的长度。
输出格式
说明/提示
1. 选择第 $2, 3, 4$ 根小木棍,长度之和为 $2 + 3 + 4 = 9$,长度最大值为 $4$;
2. 选择第 $2, 4, 5$ 根小木棍,长度之和为 $2 + 4 + 5 = 11$,长度最大值为 $5$;
3. 选择第 $3, 4, 5$ 根小木棍,长度之和为 $3 + 4 + 5 = 12$,长度最大值为 $5$;
4. 选择第 $1, 2, 3, 4$ 根小木棍,长度之和为 $1 + 2 + 3 + 4 = 10$,长度最大值为 $4$;
5. 选择第 $1, 2, 3, 5$ 根小木棍,长度之和为 $1 + 2 + 3 + 5 = 11$,长度最大值为 $5$;
6. 选择第 $1, 2, 4, 5$ 根小木棍,长度之和为 $1 + 2 + 4 + 5 = 12$,长度最大值为 $5$;
7. 选择第 $1, 3, 4, 5$ 根小木棍,长度之和为 $1 + 3 + 4 + 5 = 13$,长度最大值为 $5$;
8. 选择第 $2, 3, 4, 5$ 根小木棍,长度之和为 $2 + 3 + 4 + 5 = 14$,长度最大值为 $5$;
9. 选择第 $1, 2, 3, 4, 5$ 根小木棍,长度之和为 $1 + 2 + 3 + 4 + 5 = 15$,长度最大值为 $5$。### 【样例 2 解释】共有以下 $6$ 种选择小木棍的方案,使得选出的小木棍能够拼成一个多边形:
1. 选择第 $1, 2, 3$ 根小木棍,长度之和为 $2 + 2 + 3 = 7$,长度最大值为 $3$;
2. 选择第 $3, 4, 5$ 根小木棍,长度之和为 $3 + 8 + 10 = 21$,长度最大值为 $10$;
3. 选择第 $1, 2, 4, 5$ 根小木棍,长度之和为 $2 + 2 + 8 + 10 = 22$,长度最大值为 $10$;
4. 选择第 $1, 3, 4, 5$ 根小木棍,长度之和为 $2 + 3 + 8 + 10 = 23$,长度最大值为 $10$;
5. 选择第 $2, 3, 4, 5$ 根小木棍,长度之和为 $2 + 3 + 8 + 10 = 23$,长度最大值为 $10$;
6. 选择第 $1, 2, 3, 4, 5$ 根小木棍,长度之和为 $2 + 2 + 3 + 8 + 10 = 25$,长度最大值为 $10$。
### 【样例 3】
见选手目录下的 $polygon/polygon3.in$ 与 $polygon/polygon3.ans$。
该样例满足测试点 $7 \sim 10$ 的约束条件。
### 【样例 4】
见选手目录下的 $polygon/polygon4.in$ 与 $polygon/polygon4.ans$。
该样例满足测试点 $11 \sim 14$ 的约束条件。
### 【子任务】
对于所有测试数据,保证:
– $3 \leq n \leq 5,000$;
– 对于所有 $1 \leq i \leq n$,均有 $1 \leq a_i \leq 5\,000$。
::cute-table{tuack}
| 测试点编号 | $n \leq$ | $\max_{i=1}^{n} a_i \leq$ |
| :–: | :–: | :–: |
| $1 \sim 3$ | $3$ | $10$ |
| $4 \sim 6$ | $10$ | $10^2$|
| $7 \sim 10$ | $20$ | ^ |
| $11 \sim 14$ | $500$ | ^ |
| $15 \sim 17$ | ^ | $1$ |
| $18 \sim 20$ | $5\,000$ | ^ |
| $21 \sim 25$ | ^ | $5\,000$ |
解题思路
暴力可得50:f[i][j][k]表示前i根木棍最大值为j总长为k的方案,会超时,记忆化搜索不断优化可得68、80、100。
可以对木棍进行排序,从小到大枚举最长木棍。由于木棍总长很大,我们处理不合法方案——长度不超过5000的方案数。
对于第i根木棍,长度为a[i],之前的木棍凑出长度不超过a[i]跟他搭配都是不合法的。超过a[i]都是合法的,因为必定至少2根。
程序实现
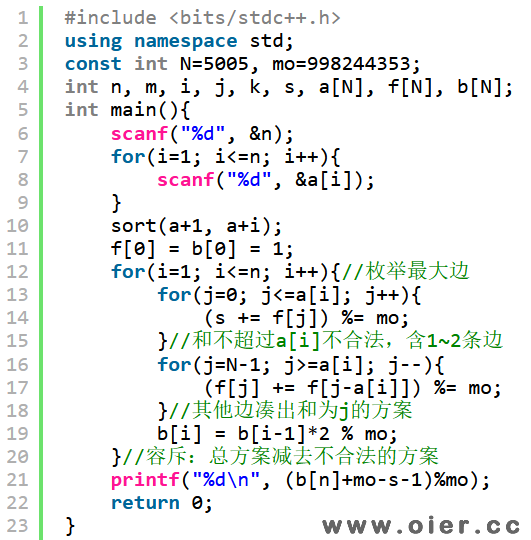
原来是这样用的 😉