洛谷P1796汤姆斯的天堂梦[NOI导刊]
1185+
作者：crxis 发布：2021-05-10 分类：动态规划
题目大意：有n级星球，每级星球有若干个，相邻级别星球间有有向道路，请问从0级星球，到达n级星球，最小花费是多少？
题目描述
汤姆斯生活在一个等级为 $0$ 的星球上。那里的环境极其恶劣，每天 $12$ 小时的工作和成堆的垃圾让人忍无可忍。他向往着等级为 $N$ 的星球上天堂般的生活。
有一些航班将人从低等级的星球送上高一级的星球，有时需要向驾驶员支付一定金额的费用，有时却又可以得到一定的金钱。
汤姆斯预先知道了从 $0$ 等级星球去 $N$ 等级星球所有的航线和需要支付（或者可以得到）的金钱，他想寻找一条价格最低（甚至获得金钱最多）的航线。
输入输出格式
输入格式
第一行一个正整数 $N$（$N \le 100$），接下来的数据可分为 $N$ 个段落，每段的第一行一个整数 $K_i$（$K_i \le 100$），表示等级为 $i$ 的星球有 $K_i$ 个。
接下来的 $K_i$ 行中第 $j$ 行依次表示与等级为 $i$，编号为 $j$ 的星球相连的等级为 $i – 1$ 的星球的编号和此航线需要的费用（正数表示支出，负数表示收益，费用的绝对值不超过 $1000$）。
每行以 $0$ 结束，每行的航线数 $\le 100$。
输出格式
输出所需（或所得）费用。正数表示支出，负数表示收益。
输入输出样例
输入样例 #1
3
2
1 15 0
1 5 0
3
1 -5 2 10 0
1 3 0
2 40 0
2
1 1 2 5 3 -5 0
2 -19 3 -20 0输出样例 #1
-1说明
对于 $100 \%$ 的数据，$1 \le N \le 100$，$1 \le K_i \le 100$。
样例解释：
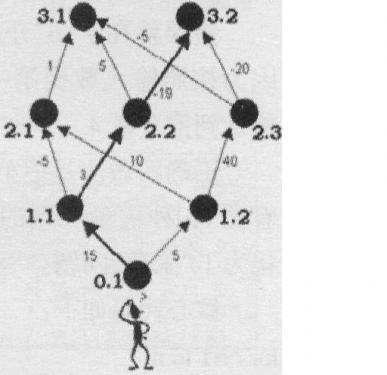
解题思路
显然，这是一个有向无环图，按照顺序递推即可。由于输入是按照低级到高级顺序的，我们可以边输入，边递推，关键是理解好样例、输入格式。
程序实现
