题目大意:n行n列方阵,从左下角走到右下角,每走1步需要耗费时间m,每走3步需要耗费a[i][j]时间,请问到达右下角,最小耗时是多少?
题目描述
Why did the cow cross the road? Well, one reason is that Farmer John’s farm simply has a lot of roads, making it impossible for his cows to travel around without crossing many of them.
奶牛们为什么要穿马路?一个原因只是因为FJ的牧场的路实在是太多了,使得奶牛们每天不得不穿梭在许许多多的马路中央
FJ’s farm is arranged as an $N \times N$ square grid of fields ($3 \leq N \leq 100$), with a set of $N-1$ north-south roads and $N-1$ east-west roads running through the interior of the farm serving as dividers between the fields. A tall fence runs around the external perimeter, preventing cows from leaving the farm. Bessie the cow can move freely from any field to any other adjacent field (north, east, south, or west), as long as she carefully looks both ways before crossing the road separating the two fields. It takes her $T$ units of time to cross a road ($0 \leq T \leq 1,000,000$).
FJ的牧场可以看作是一块 $N\times N$ 的田地($3\le N\le 100$),$N-1$ 条南北向的道路和 $N-1$ 条东西向的道路贯穿整个牧场,同时是每块田野的分界线。牧场的最外面是一圈高大的栅栏以防止奶牛离开牧场。Bessie只要穿过分离两块田野的道路,就可以从任何田野移动到与其相邻的田野里去(北,东,南或西)。当然,Bessie穿过每一条马路都是需要$T$ 时间的。($0\le T\le 1,000,000$)
One day, FJ invites Bessie to visit his house for a friendly game of chess. Bessie starts out in the north-west corner field and FJ’s house is in the south-east corner field, so Bessie has quite a walk ahead of her. Since she gets hungry along the way, she stops at every third field she visits to eat grass (not including her starting field, but including possibly the final field in which FJ’s house resides). Some fields are grassier than others, so the amount of time required for stopping to eat depends on the field in which she stops.
有一天,FJ邀请Bessie来他家下棋,Bessie从牧场的西北角出发,FJ的家在牧场的东南角。因为Bessie在中途可能会饿,所以她每走过三块田野就要停下来,享用她所在田野上的新鲜的牧草(不包括Bessie的出发点,但是可能会包括终点FJ的家),牧场上有些田野的牧草长得比其他地方茂盛,所以Bessie对应的停留时间也会变长。
Please help Bessie determine the minimum amount of time it will take to reach FJ’s house.
请帮帮Bessie计算出她走到FJ家的最短时间。
输入输出格式
输入格式
The first line of input contains $N$ and $T$. The next $N$ lines each contain $N$ positive integers (each at most 100,000) describing the amount of time required to eat grass in each field. The first number of the first line is the north-west corner.
接下来 $N$ 行,每行 $N$ 个数表示每块田野Bessie需要停留的时间(每块最多不超过$100,000$),第一行的第一块田野是牧场的西北角
输出格式
Print the minimum amount of time required for Bessie to travel to FJ’s house.
一行一个整数表示Bessie走到FJ家的最短时间
输入输出样例
输入样例 #1
4 2
30 92 36 10
38 85 60 16
41 13 5 68
20 97 13 80输出样例 #1
31说明
The optimal solution for this example involves moving east 3 squares (eating the “10”), then moving south twice and west once (eating the “5”), and finally moving south and east to the goal.
对于样例,Bessie先向东走过了三块田野(在“10”停留),再向南走两步,又向西走了一步(在“5”停留),最后向南走一步,再向东走一步到达FJ的家(不用停留),总共时间是15(停留时间)+16(穿马路时间)=31
感谢@jzqjzq 提供翻译
解题思路
深搜记忆化36,启发式搜索(优先走右下方向)72,广搜、倒搜满分。
程序实现
爆搜搜索,然后记忆化剪枝,可得36分。
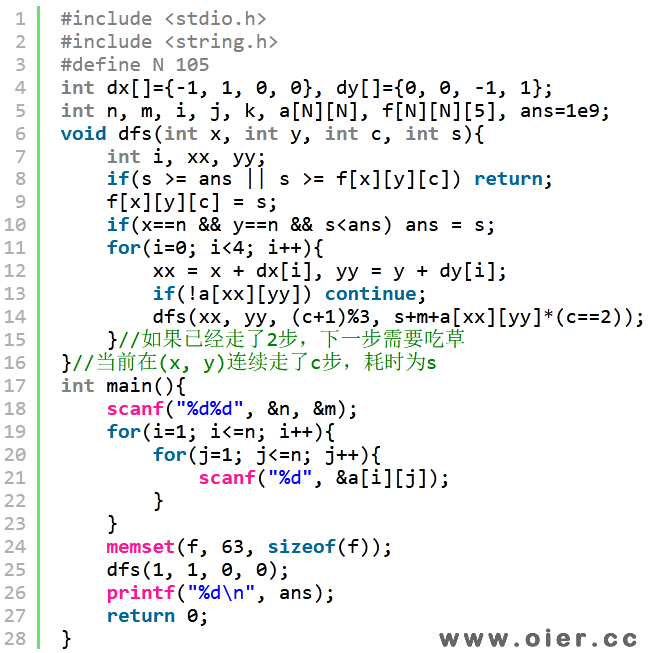
优先走右下方向,可以更快到达终点,最优性剪枝效果更好,可得72分。
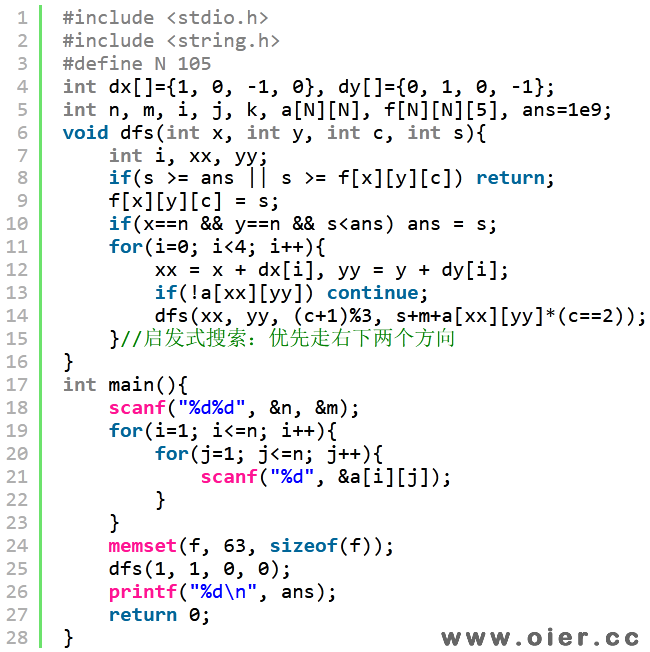
记录步数即无环,改成倒搜可得满分。步数限制应该是n*(n+1)/2,128M内存开不了那么大。

广搜比深搜快,轻松满分。
