题目大意:n个结点的树,每个点有个权值,现在需要在某些点上设定一个费用,要使每个结点都要被两个费用不小于权值的点的最短路径包含,最小费用是多少?
题意翻译
给定一棵包含 $n$ 个点的树,第 $i$ 个点的高度为 $h_i$。你可以在这 $n$ 个点中建任意多个塔,对于每个塔,你都可以指定其所在的点的编号及其势能。建一个势能为 $e$ 的塔需要花费 $e$ 枚硬币(需要保证 $e>0$)。
对于一个树上的点 $x$,我们称其接收到了信号,当且仅当在树上存在两个建了塔的点 $u,v$(需要保证 $u\neq v$,但不需要保证 $x\neq u$ 或 $x\neq v$),使得 $x$ 在从 $u$ 到 $v$ 的路径上,且 $\min(e_u,e_v)\geqslant h_x$。
请求出最少需要花费多少枚硬币,才能使得树上所有点都能接受到信号。
数据范围:
– $2\leqslant n\leqslant 2\times 10^5$。
– $1\leqslant h_i\leqslant 10^9$。
Translated by Eason_AC
题目描述
You are given a tree with $ n $ vertices numbered from $ 1 $ to $ n $ . The height of the $ i $ -th vertex is $ h_i $ . You can place any number of towers into vertices, for each tower you can choose which vertex to put it in, as well as choose its efficiency. Setting up a tower with efficiency $ e $ costs $ e $ coins, where $ e > 0 $ .
It is considered that a vertex $ x $ gets a signal if for some pair of towers at the vertices $ u $ and $ v $ ( $ u \neq v $ , but it is allowed that $ x = u $ or $ x = v $ ) with efficiencies $ e_u $ and $ e_v $ , respectively, it is satisfied that $ \min(e_u, e_v) \geq h_x $ and $ x $ lies on the path between $ u $ and $ v $ .
Find the minimum number of coins required to set up towers so that you can get a signal at all vertices.
输入输出格式
输入格式
The first line contains an integer $ n $ ( $ 2 \le n \le 200\,000 $ ) — the number of vertices in the tree.
The second line contains $ n $ integers $ h_i $ ( $ 1 \le h_i \le 10^9 $ ) — the heights of the vertices.
Each of the next $ n – 1 $ lines contain a pair of numbers $ v_i, u_i $ ( $ 1 \le v_i, u_i \le n $ ) — an edge of the tree. It is guaranteed that the given edges form a tree.
输出格式
输入输出样例
输入样例 #1
3
1 2 1
1 2
2 3输出样例 #1
4输入样例 #2
5
1 3 3 1 3
1 3
5 4
4 3
2 3输出样例 #2
7输入样例 #3
2
6 1
1 2输出样例 #3
12说明
In the first test case it’s optimal to install two towers with efficiencies $ 2 $ at vertices $ 1 $ and $ 3 $ .
In the second test case it’s optimal to install a tower with efficiency $ 1 $ at vertex $ 1 $ and two towers with efficiencies $ 3 $ at vertices $ 2 $ and $ 5 $ .
In the third test case it’s optimal to install two towers with efficiencies $ 6 $ at vertices $ 1 $ and $ 2 $ .
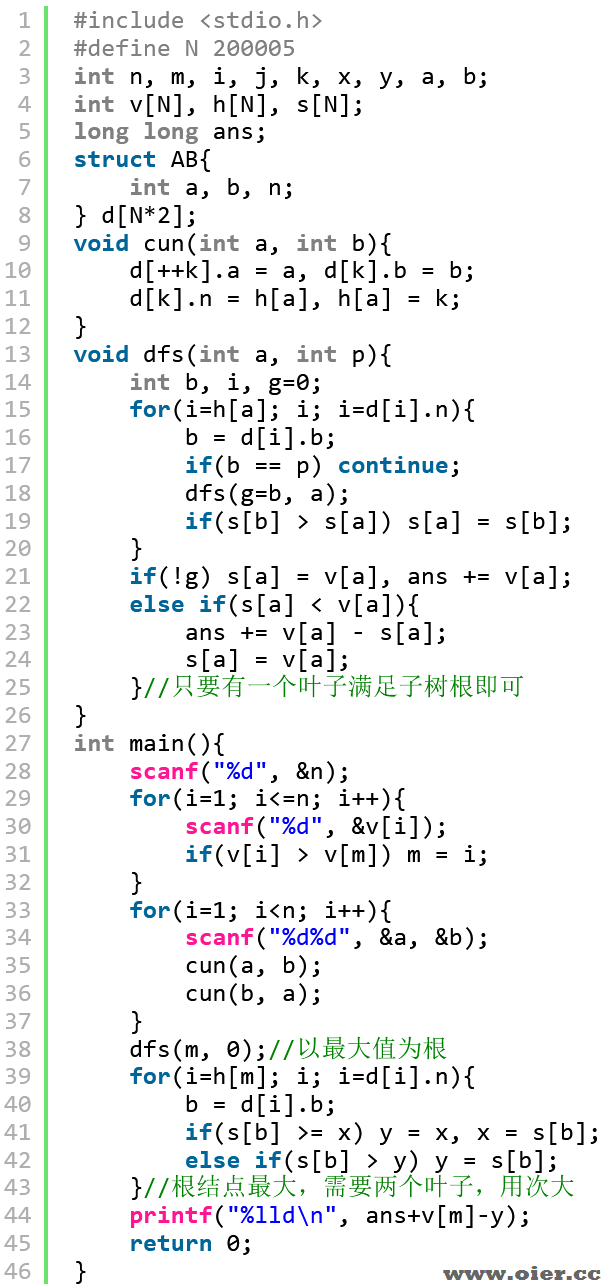
解题思路
每个点都要被包含,要么在子树内解决,要么一个在子树内,一个在外面。
什么时候在外面?外面有一个更大的点!那我们就让外面有一个更大的点,直接以最大点为根!这样,子树内只需要选择一个点不小于子树根的权值即可。
不难发现,费用都放在叶子节点,这是显而易见的贪心——往下放路径更长、费用等价。我们可以先让叶子结点的费用等于权值,从下往上,遇到更小的父亲没问题,遇到更大的父亲,则父亲需要更大的叶子,改哪个?该最大的费用差最小。
结论:以最大权值点为跟,除了根结点,每个结点只需要在子树找一个叶子满足权值即可,因为上面还有一个大权值点。根结点则需要找两个叶子节点,找最大和次大费用最小。
程序实现