题目大意:给定两个正整数,求它们的最大公约数(请使用辗转相除法)。
输入
输出
样例输入
6 9
样例输出
3
解题思路
求最大公约数可以使用辗转相除法:如果a > b > 0,那么a和b的最大公约数等于b和a%b的最大公约数,问题会逐渐变小,直到a%b等于0的时候,b的值就是所要求的最大公约数。
比如:9和6的最大公约数等于6和9%6=3的最大公约数,由于6%3==0,所以最大公约数为3。
代码中没有判断a和b的大小,因为如果b比a大,b和a%b就自动转换成了b和a,让大的放到前面。
程序实现

暴力枚举,时间复杂度O(b),如果b很大,会超时。如果不会高级方法,只能如此:从1到b逐个数字试探,如果既是a的约数,也是b的约数,那么就是a和b的公约数,从小到大枚举,最后发现的公约数就是最大公约数。

更相减损术:两个正整数a和b(a>b),它们的最大公约数等于a-b的差值c和较小数b的最大公约数(a和b的最大公约数,与a和a+b的最大公约数相同)。这样,一直减下去,最值小的那个数会编程0,次数大的那个数就是最大公约数了。当然,a == b时也可以结束循环了。最坏的时间复杂度是O(a)。

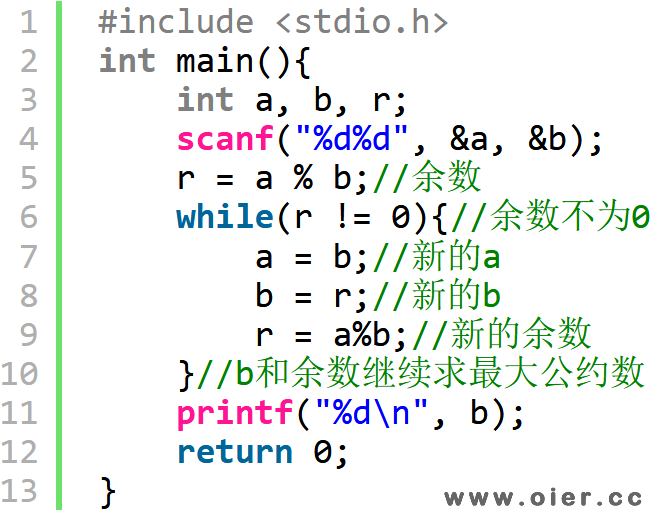
辗转相除法:一直减的话,在极端情况下也会变慢,如a=999999999,b=1,这样就需要减999999999次了!大的数a减小的数b,最终必会将a减到a%b,因此我们可以用模运算减少循环次数。时间复杂度O(log(b))。
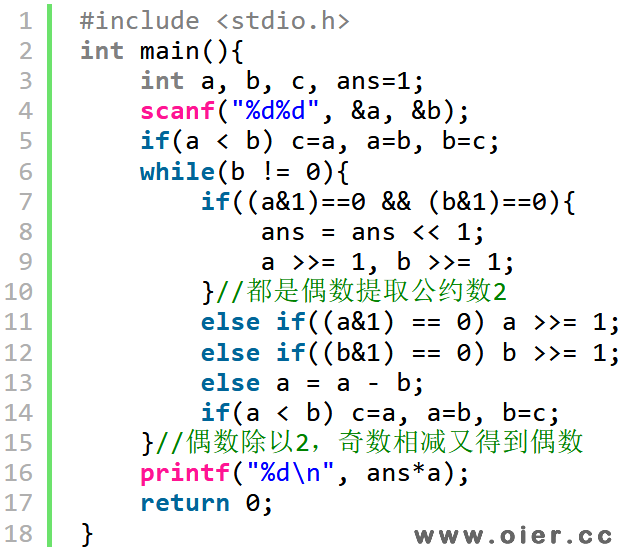
位运算优化:模运算比较慢,尤其是大整数。我们可以在更相减损术的基础上,结合位运算和辗转相除法,得到一个效率更稳定的二进制算法。同样是大数a减去小数b,如果发现a和b都是偶数,就先提取公因子2,再一起除以2;如果只有一个是偶数,那么偶数直接除以2,因为这个因子2不是公约数;如果都是奇数,那才相减,相减后,必会得到一个偶数!因为每次减法都得到一个偶数,出现偶数就会除以2,最多除以log次2,因此时间复杂度是O(log(a))。